|
|
|
| Title | Find solutions to the equilateral triangle puzzle in Visual Basic 6 |
|---|
| Description | This example shows how to find solutions to the equilateral triangle puzzle in Visual Basic 6. |
|---|
| Keywords | algorithms, games, graphics, mathematics, example, example program, Windows Forms programming, Visual Basic 6, VB 6 |
|---|
| Categories | Algorithms, Algorithms, Puzzles and Games |
|---|
|
|
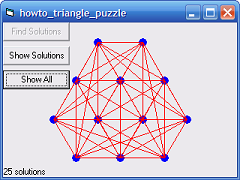
This program uses the following code to find the solutions to the puzzle Puzzle: find the equilateral triangles in Visual Basic 6.
|
|
' Find the solutions.
Private Sub cmdFindSolutions_Click()
Const tiny As Double = 0.0001
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim dx_ij As Double
Dim dy_ij As Double
Dim dist_ij As Double
Dim dx_jk As Double
Dim dy_jk As Double
Dim dist_jk As Double
Dim dx_ki As Double
Dim dy_ki As Double
Dim dist_ki As Double
Set Solutions = New Collection
For i = 1 To Xs.Count
For j = i + 1 To Xs.Count
dx_ij = Xs(j) - Xs(i)
dy_ij = Ys(j) - Ys(i)
dist_ij = Sqr(dx_ij * dx_ij + dy_ij * dy_ij)
For k = j + 1 To Xs.Count
dx_jk = Xs(k) - Xs(j)
dy_jk = Ys(k) - Ys(j)
dist_jk = Sqr(dx_jk * dx_jk + dy_jk * dy_jk)
If (Math.Abs(dist_ij - dist_jk) < tiny) Then
dx_ki = Xs(i) - Xs(k)
dy_ki = Ys(i) - Ys(k)
dist_ki = Sqr(dx_ki * dx_ki + dy_ki * _
dy_ki)
If (Math.Abs(dist_jk - dist_ki) < tiny) _
Then
' This is a solution.
AddSolution i, j, k
End If
End If
Next k
Next j
Next i
lblNumSolutions.Caption = Solutions.Count & " solutions"
cmdFindSolutions.Enabled = False
cmdShowSolutions.Enabled = True
cmdShowAllSolutions.Enabled = True
CurrentSolution = Solutions.Count + 1
Refresh
End Sub
|
|
|
The code loops through all of the points three times. Each loop starts at the point after the point used in the enclosing loop so the innermost loop only considers each triple of points once and the points in each triple are unique. In other words, the code doesn't look at triples that contain the same point more than once.
The code calculates the distances between the pairs of points in each triple and, if the distances are the same, adds a new triangle holding the points to the solution list.
Note that the distances are floating point values and rounding errors often make floating point values not exactly equal when they should be the same. This is a common problem when working with floating point numbers that should be the same. To avoid problems with equality testing, the code subtracts two distances, takes the absolute value, and checks whether the result is close to 0.
(This example defines the comparison value tiny to be 0.0001. In fact, this example is measuring distances in pixels so you could define tiny to be 1 and you would still find the correct solutions.)
Related links:
|
| |
|
|
| |
| |
 |
| |
|
|
